ASTRONOMICAL FORMULAE / FORMULAE FOR TELESCOPES
9/87v3.5
APERTURE D = F/f
- where D is the aperture of the objective
F is the focal length of the objective
f is the f-number (f/D) of the objective
MAGNIFICATION: BY FIELDS M = Alpha/Theta
- where M is the magnification
Alpha is the apparent field
Theta is the true field
Apparent Field: the closest separation eye can see is 4 minutes
of arc, more practically 8-25 minutes, 1-2 minutes for good eyes.
The Zeta Ursae Majoris double (Mizar/Alcor) is 11.75 minutes;
Epsilon Lyrae is 3 minutes.
True Field (in degrees) = 0.25 * time * cos of the declination
True Field (in minutes) = 15 * time * cos of the declination
where time is the time to cross the ocular field in minutes
A star therefore has an apparent motion westward at the following
rates:
15 degrees /h (1.25 degrees/5 min) at 0 degrees declination
13 degrees /h (1.08 degrees/5 min) at 30 degrees declination
7.5 degrees /h (0.63 degrees/5 min) at 60 degrees declination.
MAGNIFICATION: BY FOCAL LENGTHS: M = F/f
- where M is the magnification
F is the focal length of the objective
f is the focal length of the ocular
At prime focus (ground glass), magnification is 1x for each 25
mm of F
MAGNIFICATION: BY DIAMETER AND EXIT PUPIL: M = D/d
- where M is the magnification
D is the diameter of the objective
d is the exit pupil (5-6 mm is best; 7 mm not produce a sharp outer image)
EXIT PUPIL: d = f/f-number
- (by substituting F/f for M) where d is the exit pupil
f is the focal length of the ocular
f-number is the f-number (f/) of the objective
By substituting d=7 (the scotopic aperture of the human pupil)
and multiplying it by the f-number, the longest useful focal length
of the ocular is given.
LOW-POWER LAW FOR LIMITING MAGNIFICATION: M = D/6 = 0.17*D
- (by substituting 6 mm for d and taking the reciprocal) where
M is the minimum magnification without wasting light for a dark-adapted
eye (0.17x per mm of aperture)
D is the diameter of the objective in mm
HIGH-POWER LAW FOR LIMITING MAGNIFICATION
M = D/0.63 = 1.58*D
(by substituting 0.63 mm, the minimum diameter to which the average
human pupil can contract, for d and taking the reciprocal)
- where M is the maximum theoretical magnification (1.58x per
mm of aperture);
the maximum practical magnification is +50%).
LIMITING VISUAL MAGNITUDE (LIGHT-GATHERING POWER)
m = 6.5-5 log Delta + 5 log D
= 2.7+5 log D (assuming transparent dark-sky conditions and magnification
> = 1D in mm)
- where m is the approximate limiting visual magnitude
Delta is the pupillary diameter in mm (accepted value 7.5)
D is the diameter of the objective in mm
ANGULAR RADIUS OF AIRY (DIFFRACTION) DISC
r = (1.12*Lambda*206265)/D
= 127.1/D
(the second formula is based on Lambda = 0.00055 for yellow light)
- where r is the angular radius (one-half the angular diameter)
of the Airy disc (irreducible minimum size of a star disc) in
seconds of arc
Lambda is the wavelength of the light in mm
206265 is the number of seconds of arc in a radian
D is the diameter of the objective in mm
The Airy disc in visual appearance is brighter at the center,
dimmer at the edges.
LINEAR RADIUS OF AIRY (DIFFRACTION) DISC
r = 0.043*Lambda*f
- where r is the linear radius (one-half the linear diameter)
of the Airy disc in mm (change 1.12 to 0.043 for inches)
Lambda is the wavelength of light in mm (yellow light 0.00055)
f is the f-number (f/) of the objective
DEPTH OF FIELD (PHOTOVISUAL)
c = (Distance*Lambda)/D^2
- where c is the depth of field in mm
Distance is that to the objective from the object viewed or imaged (in mm)
Lambda is the wavelength of light in mm (yellow light 0.00055 for peak of human visual sensitivity)
D is the diameter of the objective in mm
Note: this formula is a good approximation valid for our Questar Long Distance Microscopes too.
DAWES LIMIT (SMALLEST RESOLVABLE ANGLE, RESOLVING POWER)
Theta = 115.8/D
- where Theta is the smallest resolvable angle in seconds of
arc
D is the diameter of the objective in mm
Atmospheric conditions seldom permit Theta 0.5 seconds of arc.
The Dawes Limit is one-half the angular diameter of the Airy (diffraction)
disc, so that the edge of one disc does not extend beyond the
center of the other). The working value is two times the Dawes
Limit (diameter of the Airy disc), so that the edges of the two
stars are just touching.
MAGNIFICATION NEEDED TO SPLIT A DOUBLE STAR
M = 480/d
- where M is the magnification required
480 is number of seconds of arc for an apparent field of 8 minutes of arc
d is the angular separation of the double star
About the closest star separation that the eye can distinguish
is 4 minutes of arc (240 seconds of arc). Twice this distance,
or an 8-minute (480 seconds) apparent field angle, is a more practical
value for comfortable viewing. In cases where the comes is more
than five magnitudes fainter than the primary, you will need a
wider separation: 20 or 25 minutes of arc, nearly the width of
the moon seen with the naked eye.
RESOLUTION OF LUNAR FEATURES
Resolution = (2*Dawes Limit*3476)/1800)
Dawes Limit * 3.88
- where Resolution is the smallest resolvable lunar feature
in km
2*Dawes Limit is the Airy disc (a more practical working value is twice this)
1800 is the angular size of the moon in seconds of arc
3476 is the diameter of the moon in km
LIGHT GRASP: Light Grasp = (D/d)^2*Pi
- = 7*D^2
- where Light Grasp is times that received by the retina
D is the diameter of the objective in mm
d is the diameter of the eye's pupillary aperture in mm (accepted value 7.5)
pi is the transmission factor (approximately equal to 62.5% for the average telescope, up to approximately 180 mm)
To compare the relative light grasp of two main lenses used at
the same magnification, compare the squares of their effective
diameters ("effective" considers obstructions, surface
smoothness, transmission and reflectivity).
FORMULAE FOR ASTROPHOTOGRAPHY
F-NUMBER: PRIME FOCUS (ERECT IMAGE)
f/ = F/D
- where f/ is the f-number of the system (objective)
F is the focal length of the objective
D is the diameter of the objective
F-NUMBER: AFOCAL, EYEPIECE-CAMERA LENS (REVERSED IMAGE)
f/ = F minutes/D
= (M*Fc)/D
= ((F/Fe)*Fc)/D
= (F/D)*(Fc/Fe)
= (M/D)*Fc
- where f/ is the f-number of the system
F minutes is the effective focal length of the system
Fe is the focal length of the ocular (divided by any Barlow magnification)
D is the diameter of the objective
M is the magnification
Fc is the focal length of the camera
F is the focal length of the objective
Fc/Fe is the projection magnification
M/D is the power per mm
The diameter of the first image equals the film diagonal (44 mm
for 35 mm film) divided by the magnification.
F-NUMBER: EYEPIECE PROJECTION, POSITIVE LENS (REVERSED IMAGE)
f/ = F minutes/D
= (F/D)*(B/A)
= (F/D)*(((M+1)*Fe)/A)
= (F/D)*((B/Fe)-1)
- where f/ is the f-number of the system
F minutes is the effective focal length of the system
D is the diameter of the objective
F is the focal length of the objective (times any Barlow magnification)
B is the secondary image ("throw"), the distance of the ocular center from the focal plane of the film, equal to ((M+1)*Fe)/A
A is the primary image, the distance of the ocular center from the focal point of the telescope objective
M is the projection magnification, equal to (B/Fe)-1
Fe is the focal length of the ocular
F-NUMBER: NEGATIVE LENS PROJECTION (ERECT IMAGE)
f/ = F minutes/D = (F/D) * (B/A)
- where f/ is the f-number of the system
F minutes is the effective focal length of the system
D is the diameter of the objective
B is the distance of the Barlow center from the focal plane of the film
A is the distance of the Barlow center from the focal point of the telescope objective
B/A is the projection magnification (Barlow magnification)
EXPOSURE COMPARISON FOR EXTENDED OBJECTS
= (f/S)^2/(f/E)^2 = ((f/S)/(f/E))^2
(the ratio of intensities of illumination is squared according
to the inverse square law)
- where Exposure Compensation is the exposure compensation to
be made to the example system
f/S is the f-number (f/) of the subject system
f/E is the f-number (f/) of the example system
EXPOSURE COMPARISON FOR POINT SOURCES
= De^2/Ds^2 = (De/Ds)^2
- where Exposure Compensation is the exposure compensation to
be made to the example system
De is the objective diameter of the example system
Ds is the objective diameter of the subject system
LIGHT-RECORDING POWER OF A SYSTEM: Power = r^2/f^2
(the light-recording power is directly proportional to the square
of the radius of the objective and inversely proportional to the
square of the f-number)
- where Power is the light-recording power of the system
r is the radius of the objective
f is the f-number (f/) of the system
Example: a 200-mm f/8 system compared with a 100-mm f/5 system
(100^2)/8^2 compared with (50^2)/5^2
156.25 compared with 100, or 1.56 times more light-recording power
PRINT'S EFFECTIVE FOCAL LENGTH
Print EFL = Camera FL * Print Enlargement
- where Print EFL is the print 's effective focal length
Camera F. L. is the camera 's focal length
Print Enlargement is the amount of enlargement of the print (3x is standard for 35mm film)
GUIDESCOPE MAGNIFICATION
Guidescope M = about f/12.5
- where Guidescope M is the magnification needed for guiding
astrophotographs
f is the photographic focal length in mm
Experience indicates that the minimum guiding magnification needed
is about f divided by 12.5, precisely what a 12.5 mm guiding ocular
used in an off-axis guider for prime-focus photography yields.
Since visual magnification is the ratio of the objective to ocular
focal length, the combination of prime-focus camera and off-axis
guider with a 12.5-mm ocular gives a guiding magnification of
f/12.5. f/7.5 (as with a typical focal reducer that reduces the
effective focal length by a factor of 0.6); this is a significant
improvement. f/5 or higher magnification is for top-quality guiding.
Guidescope M = Guidescope EFL / Print EFL
- where Guidescope M is the guidescope's magnification (should
be >= 1, preferably 5-8)
Guidescope EFL is the guidescope's effective focal length, the guidescope's focal length times any Barlow magnification (should be >= to the focal length of the primary and the guidescope's magnification, 0.2x per mm of focal length of the objective, 0.1x per mm of the camera lens
Print EFL is the print 's effective focal length
GUIDING TOLERANCE
Guiding Tolerance = 0.076 * Guidescope M
- where Guiding Tolerance is in mm
0.076 is 1 second of arc at a 254-mm reading distance from the print (a cross hair web is about 0.05 mm)
MAXIMUM ALLOWABLE TRACKING (SLOP) ERROR
S = about 8250/(F*E)
- where S is the error ("slop") in seconds of arc
F is the focal length in mm
E is the amount of enlargement of the print (3x is the standard for 35-mm film)
The slop is derived from the formula Theta = K*(h/F), with K =
206265 (the number of seconds in a radian) and h = 0.04 mm of
image-drift tolerance (an empirical value from astrophotographs).
CONVERSION OF PLATE SCALE TO EFFECTIVE FOCAL LENGTH
EFL = mm per degree * 57.3 = 206265/seconds of arc per mm
- where EFL is the effective focal length in mm
57.3 is the number of degrees in a radian
206265 is the number of seconds of arc in a radian
RESOLVING POWER OF A PHOTOGRAPHIC SYSTEM
Resolving Power = 4191 seconds of arc/F (For Tech Pan R = 660
seconds/F)
- where Resolving Power is that of a photographic system with
Kodak 103a or color film
F is the focal length of the system in mm
MAXIMUM RESOLUTION FOR A PERFECT LENS
Maximum Resolution = 1600/f
- where Maximum Resolution is the maximum resolution for a perfect
lens f is the f-number (f/) of the lens
Most films, even fast ones, resolve only 60 lines/mm; the human
eye resolves 6 lines/mm (less gives a "wooly" appearance).
80 lines/mm for a 50-mm lens is rated excellent (equal to 1 minute
of arc); a 200-mm lens is rated excellent with 40 lines/mm. 2415
films yields 320 line pairs (160 lines)/mm (equal to 1 second
of arc); Kodak Tri-X yields 80 lines/mm.
MINIMUM RESOLUTION NECESSARY FOR FILM
Minimum Resolution = Maximum Resolution * Print Enlargement
- where Minimum Resolution is the minimum resolution necessary
for film
Maximum Resolution is the maximum resolution for a perfect lens
Print Enlargement is the amount of enlargement of the print (3x is standard for 35mm film)
APPARENT ANGULAR SIZE OF AN OBJECT
Apparent Angular Size = (Linear Width / Distance) * 57.3
- where Apparent Angular Size is the apparent angular size of
the object in degrees
Linear Width is the linear width of the object in m
Distance is the distance of the object in m
A degree is the apparent size of an object whose distance is 57.3
times its diameter.
SIZE OF IMAGE (CELESTIAL)
h = (Theta*F)/K
Theta = K*(h/F)
F = (K*h)/Theta
- where h is the linear height in mm of the image at prime focus
of an objective or a telephoto lens
Theta is the object 's angular height (angle of view) in units corresponding to K
F is the effective focal length (focal length times Barlow magnification) in mm
K is a constant with a value of 57.3 for Theta in degrees, 3438 in minutes of arc, 206265 for seconds of arc (the number of the respective units in a radian)
The first formula yields image size of the sun and moon as approximately
1% of the effective focal length (Theta/K = 0.5/57.3 = 0.009).
The second formula can be used to find the angle of view (Theta)
for a given film frame size (h) and lens focal length (F). Example:
the 24 mm height, 36 mm width, and 43 mm diagonal of 35 mm film
yields an angle of view of 27 degrees, 41 degrees, and 49 degrees
for a 50-mm lens.
The third formula can determine effective focal length (F) required
for a given film frame size (h) and angle of view (Theta).
SIZE OF IMAGE (TERRESTRIAL)
h = (Linear Width / Distance) * F
Linear Width = (Distance * h) / F
Distance = (Linear Width * F) / h
F = (Distance * h) / Linear Width
- where h is the linear height in mm of the image at prime focus
of an objective or telephoto lens
Linear Width is the linear width of the object in m
Distance is the distance of the object in m
F is the effective focal length (focal length times Barlow magnification) in mm
LENGTH OF A STAR TRAIL ON FILM
Length = F*T*0.0044
- where Length is the length in mm of the star trail on film
F is the focal length of the lens in mm
T is the exposure time in minutes
0.0044 derives from (2*Pi)/N for minutes (N = 1440 minutes per day)
EXPOSURE TIME FOR STAR TRAIL ON 35-MM FILM
T = 5455/F
where T is the exposure time in minutes for a length of 24 mm
(the smallest dimension of 35mm film)
F is the focal length of the lens in mm
MAXIMUM EXPOSURE TIME WITHOUT STAR TRAIL
T = (1397/F)
- where T is the maximum exposure time in seconds without a
star trail
1397 derives from 1 minutes at reading distance (254 mm), the
smallest angular quantity that can be perceived by the human eye
without optical aid ("limiting resolution") and is equal
to 0.1 mm. This quantity also applies to the moon. 2-3x yields
only a slight elongation. Use 20x for a clock drive.
- F is the focal length of the lens in mm
The earth rotates 5 minutes of arc in 20 seconds, which yields
a barely detectable star trail with an unguided 50-mm lens. 2-3
minutes (8-12 secs.) is necessary for an undetectable trail, 1
minute of arc (4 secs.) for an expert exposure. Divide these values
by the proportional increase in focal length over a 50-mm lens.
For example, for 3 minutes of arc (12 secs.), a 150-mm lens would
be 1/3 (1 minute and 4 secs.) and a 1000-mm lens would be 1/20
(0.15 minutes and 0.6 secs.). Note that to compensate for these
values, the constant in the formula would be 1000 for a barely-detectable
trail, 600 for an undetectable trail, and 200 for an expert exposure.
N.B. The above formulae assume a declination of 0 degrees. For
other declinations, multiply lengths and divide exposure times
by the following cosines of the respective declination angles:
0.98 (10 degrees), 0.93 (20 degrees), 0.86 (30 degrees), 0.75
(40 degrees), 0.64 (50 degrees), 0.50 (60 degrees), 0.34 (70 degrees),
0.18 (80 degrees), 0.10 (85 degrees).
EXPOSURE DURATION FOR EXTENDED OBJECTS
E = f^2/(S*B)
- where e is the exposure duration in seconds for an image size
of >= 0.1 mm
f is the f-number (f/) of the lens
S is the film 's ISO speed
B is the brightness factor of the object (Venus 1000, Moon 125, Mars 30, Jupiter 5.7)
Thus, a 2-minute exposure at f/1.4 is equivalent to a 32-minute
exposure at f/5.6 (4 stops squared times 2 minutes). This ignores
the reciprocity failure in the film, which would mean that the
32-minute exposure would have to be even longer.
SURFACE BRIGHTNESS OF AN EXTENDED OBJECT ("B" VALUE)
B = 10^0.4(9.5-M)/D^2
- where B is the surface brightness of the (round) extended
object
M is the magnitude of the object (total brightness of the object), linearized in the formula
D is the angular diameter of the object in seconds of arc (D^2 is the surface area of the object)
EXPOSURE DURATION FOR POINT SOURCES
e = (10^0.4(M+13))/S*a^2
- where e is the exposure duration in seconds for an image size
of >= 0.1 mm
M is the magnitude of the object
S if the film 's ISO speed
a is the aperture of the objective
FOCAL LENGTH NECESSARY TO PHOTOGRAPH A RECOGNIZABLE OBJECT
F = (Distance / Linear Field) * Image Size
- where F is the focal length in mm necessary to photograph
a recognizable object
Distance is the distance of the object in m
Linear Field is the linear field of the object in m
Image Size is the image size in mm (equal to 24 mm divided by the amount of enlargement of the print [3x is the standard for 35mm film] for the smallest dimension of 35mm film)
FORMULAE REGARDING THE HUMAN EYE
The scotopic aperture (dark-adapted, ranges over about 400 to
620nm peaking at 510nm) of the human pupil is typically 6 (theoretically
7, or 5 if over age 50) mm. Since the human pupil has a focal
length of 17 mm, it is f/2.4 and yields 0.17 per mm of aperture.
2.5 mm is the photopic (light-adapted, ranges over about 400 to
750nm peaking at about 555nm) diameter of the eye.
ENTRANCE PUPIL
d is the diameter of the healthy eye 's maximum pupillary aperture
in mm (accepted value of typical young adult is 7.0-7.5). An eye
dilated with drugs may reach 9.0mm or more however, there will
be a substantial loss of resolution and depth of Field. While
growing old, the human Iris loses elastically and this number
may gradually fall to 5.0mm or less.
CONTRAST DISCRIMINATION
Detail to the eye is noticed when one region contrasts, or has
a different level of brightness, with another region. Because
of the finite wavelength of light, the eye cannot notice contrast,
or brightness changes, much finer than roughly 1/4 the wavelength
of light. This region is known as the Airy disc.
MAGNITUDE LIMIT OF UNAIDED EYE
The original Magnitude scale identified Magnitude 6 as being the
faintest observable by the average human eye. As the scale has
been revised, it is now commonly accepted that 5.5 is the faintest
typically observed. These assume good health, 7.0mm entrance pupil,
and excellent atmospheric transparency.
DAWES LIMIT (SMALLEST RESOLVABLE ANGLE, RESOLVING POWER)
Theta = 115.8/d
- where Theta is the smallest resolvable angle in seconds of
arc
d is the diameter of the entrance pupil in mm
The Dawes Limit is one-half the angular diameter of the Airy (diffraction)
disc, so that the edge of one disc does not extend beyond the
center of the other). The working value is two times the Dawes
Limit (diameter of the Airy disc), so that the edges of the two
stars are just touching. For an entrance pupil of 7.0mm, this
would produce 16.54 seconds of arc (about 1/3 minute of arc)
SMALLEST RESOLVABLE LINE PAIR
The human eye resolves 6 lines/mm (less gives a "wooly"
appearance).
MISCELLANEOUS FORMULAE
HOUR ANGLE
H = Theta - Delta
- where H is the hour angle
Theta is sidereal time
Delta is right ascension
The Hour Angle is negative east of and positive west of the meridian
(as right ascension increases eastward).
BODE'S LAW (A PROGRESSION DISCOVERED BY TITUS OF WITTENBERG,
1766)
Approximat Distance of Planets from the Sun in Astronomical
Units:
(4 + 3(2^n))/10 in AU at aphelion
- where n is the serial order of the planets from the sun (Mercury
's 2n =-2.5, Venus 's n = 0, Earth 's n = 1, asteroid belt = 2.8)
ANGULAR SIZE
Theta = (55*h)/d
- where Theta is the angular size of the object in degrees
h is the linear size of the object in m
d is the distance from the eye in m
e.g., for the width of a quarter at arm 's length: (55*0.254)/0.711 = 2 degrees
TWILIGHT PERFORMANCE
Twilight Performance = ![]() (D * M)
(D * M)
- where the greater the Twilight Performance is, the better
suited the instrument (e.g., binoculars) will be for viewing in twilight or
for astronomical use after dusk (low light conditions only). This is only valid when comparing optics of similar quality; consider for example how a 5.0 liter Ferrari engine will perform differently than a Ford 5.0 liter engine.
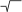 = Square Root
= Square Root
D is the diameter of the objective
M is the magnification
RELATIVE LIGHT EFFICIENCY
Relative Brightness Value = d^2 = (D/M)^2
- where the larger the relative brightness value, the better
the instrument (e.g., binoculars) is for viewing in twilight or
for astronomical use after dusk (low light conditions only). Again this is only valid when comparing optics of similar quality.
d is the diameter of the exit pupil
D is the diameter of the objective
M is the magnification
LENGTH OF A METEOR TRAIL
L = (A*D)/57.3
- where L is the linear size, or actual length in space, in
km
A is the maximum angular length as observed in degrees
D is the known altitude of the meteor as it enters the atmosphere in km
EFFICIENCY OF LENS FOR PHOTOGRAPHING AN AVERAGE METEOR
Efficiency = F/f^2
- where Efficiency is the efficiency of the lens for photographing
an average (in a meteor shower)
F is the focal length of the lens
f is the f-number (f/) of the lens
MEASURING ANGLES WITH A MICROMETER RETICLE
To calibrate a micrometer's linear scale
LS = 206265/F
- where LS is the Linear Scale division spacing) in seconds
of arc
F is the focal length of the telescope objective lens
GEOGRAPHIC DISTANCE
Geographic distance of one second of arc = 30 m * cos of the latitude
- where cos(Latitude)=1 on lines of constant longitude
ESTIMATING ANGULAR DISTANCE IN ARC DEG/MIN/SECS
For reference:
- the rotational period of the Earth is 86164.09890369732 seconds Universal Time, or 23 hours 56 minutes and 04.09890369732 seconds. The rate of rotation of the Earth is 15.04106717866910 seconds of arc per second of time.
- the mean sidereal day = 23 hours 56 minutes 04.090524 of Universal Time
- the day of Universal Time = 24 hours 03 minutes 56.5553678 of mean sidereal time
*The lengths of a day of UT and a day of mean sidereal time vary slightly with variations in the Earth's rotation. However the ratio of UT to mean sidereal time are unaffected by these variations.
| Penny, 4 km distant | 1 Second |
| Golf Ball, 6 miles (10 km) distant | 1 Second |
| Width of little finger at arm 's length | 1 degree |
| Dime at arm 's length | 1 degree |
| Quarter at arm 's length | 2.5 degrees |
| Width of fist at arm 's length | 10 degrees |
| Length of palm at arm 's length | 18 degrees |
| Width of thumb to little finger at arm 's length | 20 degrees | Sun, Moon | 30 Minutes - 1/2 Degree |
| (The Moon is about 400X smaller in angular diameter than the Sun, but is 400X closer.) | |
| Width of Orions belt | 3 degrees |
| Height of Orion | 16 degrees |
| Width of Orion Constellation | 25 degrees |
ESTIMATING VISUAL MAGNITUDES
Big Dipper, from cup to handle
| Alpha (Dubhe) | Mv = 1.9 |
| Beta (Merak) | Mv = 2.4 |
| Gamma (Phecda) | Mv = 2.5 |
| Delta (Megrez) | Mv = 3.4 |
| Epsilon (Alioth) | Mv = 1.7 - 4.9 |
| Zeta (Mizar) | Mv = 2.4 - 4.0 |
| Eta (Alkaid) | Mv = 1.9 |
Little Dipper, from cup to handle
| Beta (Kochab) | Mv = 2.2 |
| Gamma (Pherkad) | Mv = 3.1 |
| Eta | Mv = 5.0 |
| Zeta | Mv = 5.1 - 4.3 |
| Epsilon | Mv = 4.4 |
| Delta | Mv = 4.4 |
| Alpha (Polaris) | Mv = 2.1 |
RANGE OF USEFUL MAGNIFICATION OF A REASONABLE QUALITY TELESCOPE
D = diameter of aperture in mm
| Minimum useful magnification | 0.13*D (or 0.2*D for better contrast) |
| Best visual acuity | 0.25*D |
| Wide views | 0.4*D |
| Planets, general viewing | 200X or more |
| Normal high power, double stars | 1.2*D to 1.6*D |
| Close doubles | 2.35*D |
| Maximum useful magnification | 2.0*D |
| Messier objects, general viewing | 0.8*D |
| Lowest power to see all detail (resolution of eye matches that of telescope) | 0.5*D |
LPR FILTERS SUITABLE FOR VIEWING
| Filter Designation | Bandpass | Transmission | Suitable on Objects: | Opt. Exit Pupil City | Opt. E.P. Dark Site |
|---|---|---|---|---|---|
| Deep-Sky* | 90nm | 440-530nm | DN, PN, RN, SC, SG | 0.5-2mm | 1-4mm |
| H-Beta** | 9nm | 486nm | EFN | 3-7mm | 4-7mm |
| Oxygen III** | 11nm | 496 & 501nm | DN, FN, FPN, PN | 2-5mm | 3-7mm |
| Swan Band | 25nm | 495-520nm | CG, SC, PN | ||
| UHC** | 24nm | 493-509nm | DN, FN, PN | 1-4mm | 2-6mm |
*=Anti-Reflection Coated surface, **=AR Coated sandwiched filter.
LPR FILTERS SUITABLE FOR ASTROPHOTOGRAPHY
| Filter Designation | Bandpass | Transmission | Filter Factor | Suitable on Objects: | Suggested Films: |
|---|---|---|---|---|---|
| Deep Sky* | 90nm | 440-530nm | 3X to 4X | DN, EFN, FPN, PN, RN, SC, SG | Color, Black & White |
| Hydrogen-Alpha 92 | 640nm-IR | 1.5X to 3X | EFN | B&W TechPan,103aE/aF,or Infrared | |
| Minus Violet* | 420-IR | 1.1X to 1.2X | Stars, SC | Color, Black & White | |
For information, or a clarification feel free to call us.
Contents Copyright 1994-2007 Company Seven - All Rights Reserved